Balancing Moments
Moments have two possible directions, clockwise or anti-clockwise.
-If the clockwise moment is bigger than the anticlockwise moment, then the object will turn clockwise.
-If the anticlockwise moment is bigger than the clockwise moment, then the object will turn anticlockwise.
-If the clockwise moment is equal to the clockwise moment, then the object will stay where it is.
This leads to an important rule in Physics, the Principle of Moments:
If the clockwise moment = anticlockwise moment, the system is in equilibrium
This means that the system is balanced:

Conditions for equilibrium:
1.All forces on it are balanced; resultant force is zero
2.The resultant moment about the pivot is zero(must justify principle of moments)
Example with worked solutions:
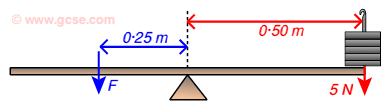
clockwise moment = anticlockwise moment
Clockwise moment = 5 N × 0·50 m = 2·50 Nm.
Anticlockwise moment = F × 0·25 m = 2·50 Nm
Force F = 2·50 Nm ÷ 0·25 m = 10 N
In order to balance the 5 N force acting at 0·5 m from the pivot, we require 10 N acting in the opposite direction but at 0·25 m.

A 5 m uniform plank weighing 600 N is placed on a level road. A man applies a force at one end. What is the minimum force required to lift it up?
A.600 N
B.900 N
C.300 N
D.12 00 N
Answer : 300N
Moment acting on plank: 2.5 x 600 = 1500Nm
Moment needed to lift plank: 1500Nm
Amount of effort needed : 1500Nm/5m = 300N
Sometimes moments can easily become unbalanced - even when we don't want them to!


In these unfortunate examples, it would seem that in loading the cart, some of the boxes must have slipped to the back - further away from the pivot - greatly increasing their turning effect. In the case of the lorry, its weight wasn't enough to balance the heavy bricks.
The result was the lifting of the donkey - who must have been very surprised! For the lorry, it was lucky nobody was hurt.
Many Moments
Sometimes more than one force acts on the same side of the pivot. Their overall turning effect is easy to work out.
2 forces, both acting clockwise, 2 N and 5 N at 0.2 m and 0.5 m respectively
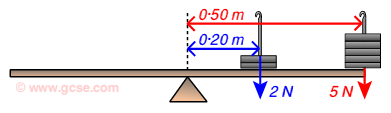
The 2 N force has a moment of 2 × 0·2 m = 0·4 Nm clockwise.
The 5 N force has a moment of 5 × 0·5 m = 2·5 Nm clockwise.
Their combined moment = 0·4 Nm + 2·5 Nm = 2·9 Nm clockwise.
Moments can just be added, but they must act in the same direction.
No comments:
Post a Comment