When a force acts upon an object to cause a displacement of the object, it is said that work was done upon the object. There are three key ingredients to work - force, displacement, and cause. In order for a force to qualify as having done work on an object, there must be a displacement and the force must cause the displacement
"Work done" is another way of saying "energy transferred".
Work done = Energy transferred.
W = E
The equation which connects work, force and distance is
Work done = Force x Distance.
W = F x d
The equation can also be written as
Energy = Force x Distance.
E = F x d
In words:
Work done by a constant force on an object is given by the product of the force and the distancce moved by the object in the direction of the force.
Whenever a new quantity is introduced in physics, the standard metric units associated with that quantity are discussed. In the case of work (and also energy), the standard metric unit is the Joule (abbreviated J). One Joule is equivalent to one Newton of force causing a displacement of one meter. In other words,
The Joule is the unit of work.
1 Joule = 1 Newton * 1 meter
1 J = 1 N * m
Cases where no work is done:
1. Work is not done when The direction of the applied force and the direction in which the object moves are perpendicular to each other.
2.Work is zero if applied force is zero (W=0 if F=0): If a block is moving on a smooth horizontal surface (frictionless), no work will be done. Note that the block may have large displacement but no work gets done.
3.Work done is zero when displacement is zero. This happens when a man pushes a wall. There is no displacement of the wall. Thus, there is no work done.
In order to accomplish work on an object there must be a force exerted on the object and it must move in the direction of the force.
In summary, work is done when a force acts upon an object to cause a displacement. Three quantities must be known in order to calculate the amount of work. Those three quantities are force, displacement and the angle between the force and the displacement.
MECHANICAL ENERGY

In the process of doing work, the object which is doing the work exchanges energy with the object upon which the work is done. When the work is done upon the object, that object gains energy. The energy acquired by the objects upon which work is done is known as mechanical energy.
The two types of Mechanical energy that a body may have are Kinetic Energy and Gravitational Potential energy.
Kinetic Energy
Kinetic energy is the energy of motion. An object which has motion - whether it be vertical or horizontal motion - has kinetic energy. Whereas An Object which is stationary does not have any kinetic energy. When a force moves an object, it does work and it gains kinetic energy.
Hence, we can see that the kinetic energy of the object is due to the work done by the force.
The amount of translational kinetic energy (from here on, the phrase kinetic energy will refer to translational kinetic energy) which an object has depends upon two variables: the mass (m) of the object and the speed (v) of the object. The following equation is used to represent the kinetic energy (KE) of an object.
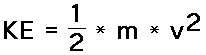
where m = mass of object
v = speed of object
This equation reveals that the kinetic energy of an object is directly proportional to the square of its speed.
Kinetic energy is a scalar quantity; it does not have a direction. Unlike velocity, acceleration, force, and momentum, the kinetic energy of an object is completely described by magnitude alone.
Like work and potential energy, the standard metric unit of measurement for kinetic energy is the Joule. As might be implied by the above equation, 1 Joule is equivalent to 1 kg*(m/s)^2.
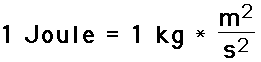
We can see that for two objects of the same mass moving at different speeds ,the faster object has a greater kinetic energy.Similarly, for two objects of different masses moving at different speeds, the object of greater mass has greater kinetic energy.
Check Your Understanding
1. Determine the kinetic energy of a 625-kg roller coaster car that is moving with a speed of 18.3 m/s.
Answer
2. If the roller coaster car in the above problem were moving with twice the speed, then what would be its new kinetic energy?
Answer
3. Missy Diwater, the former platform diver for the Ringling Brother's Circus, had a kinetic energy of 12 000 J just prior to hitting the bucket of water. If Missy's mass is 40 kg, then what is her speed?
Answer
4. A 900-kg compact car moving at 60 mi/hr has approximately 320 000 Joules of kinetic energy. Estimate its new kinetic energy if it is moving at 30 mi/hr. (HINT: use the kinetic energy equation as a "guide to thinking.")
Answer
Potential Energy
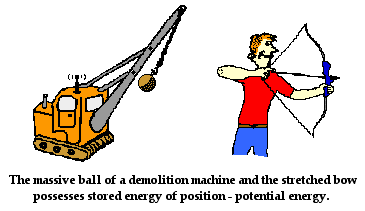
An object can store energy as the result of its position. For example, the heavy heavy ball of a demolition machine is storing energy when it is held at an elevated position. This stored energy of position is referred to as potential energy.
Similarly, a drawn bow is able to store energy as the result of its position. When assuming its usual position (i.e., when not drawn), there is no energy stored in the bow.
Yet when its position is altered from its usual equilibrium position, the bow is able to store energy by virtue of its position. This stored energy of position is referred to as potential energy. Potential energy is the stored energy of position possessed by an object.
 border="0" alt="" />
border="0" alt="" />Gravitational Potential Energy
The two examples above illustrate the two forms of potential energy to be discussed in this course - gravitational potential energy and elastic potential energy. Gravitational potential energy is the energy stored in an object as the result of its vertical position or height. The energy is stored as the result of the gravitational attraction of the Earth for the object. The gravitational potential energy of the massive ball of a demolition machine is dependent on two variables - the mass of the ball and the height to which it is raised. There is a direct relation between gravitational potential energy and the mass of an object.
These relationships are expressed by the following equation:
PEgrav = mass * g * height
PEgrav = m * g * h
In the above equation, m represents the mass of the object, h represents the height of the object and g represents the acceleration of gravity (9.8 m/s/s on Earth).
More massive objects have greater gravitational potential energy. There is also a direct relation between gravitational potential energy and the height of an object. The higher that an object is elevated, the greater the gravitational potential energy.
Since the gravitational potential energy of an object is directly proportional to its height above the zero position, a doubling of the height will result in a doubling of the gravitational potential energy. A tripling of the height will result in a tripling of the gravitational potential energy.
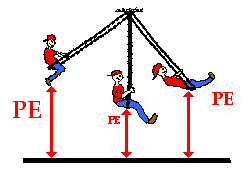
Use this principle to determine the blanks in the following diagram. Knowing that the potential energy at the top of the tall platform is 50 J, what is the potential energy at the other positions shown on the stair steps and the incline?
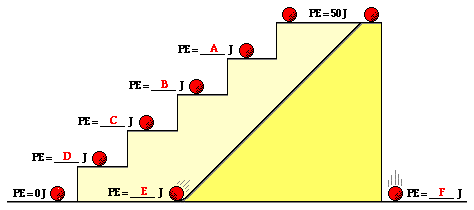
ANS
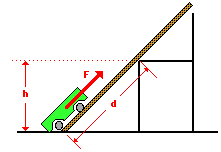
1. A cart is loaded with a brick and pulled at constant speed along an inclined plane to the height of a seat-top. If the mass of the loaded cart is 3.0 kg and the height of the seat top is 0.45 meters, then what is the potential energy of the loaded cart at the height of the seat-top?
ANS
2.2. If a force of 14.7 N is used to drag the loaded cart (from previous question) along the incline for a distance of 0.90 meters, then how much work is done on the loaded cart?
No comments:
Post a Comment