Newton's third law of motion

According to Newton, whenever objects A and B interact with each other, they exert forces upon each other. When you sit in your chair, your body exerts a downward force on the chair and the chair exerts an upward force on your body. There are two forces resulting from this interaction - a force on the chair and a force on your body. These two forces are called action and reaction forces and are the subject of Newton's third law of motion

Newton's third law of motion is:

For every action, there is an equal and opposite reaction.These forces act on mutually opposite bodies.

The statement means that in every interaction, there is a pair of forces acting on the two interacting objects. The size of the forces on the first object equals the size of the force on the second object. The direction of the force on the first object is opposite to the direction of the force on the second object. Forces always come in pairs - equal and opposite action-reaction force pairs.


Characteristics of forces:

1.Forces always come in pairs - equal and opposite action-reaction force pairs.
2.Action and reaction forces are equal in magnitude.
3.Action and reaction forces act in opposite direction.
4.Action and reaction forces act on different bodies.

Example:



A fish uses its fins to push water backwards. But a push on the water will only serve to accelerate the water. Since forces result from mutual interactions, the water must also be pushing the fish forwards, propelling the fish through the water. The size of the force on the water equals the size of the force on the fish; the direction of the force on the water (backwards) is opposite the direction of the force on the fish (forwards). For every action, there is an equal (in size) and opposite (in direction) reaction force. Action-reaction force pairs make it possible for fish to swim.

Another Example:



A bird flies by use of its wings. The wings of a bird push air downwards. Since forces result from mutual interactions, the air must also be pushing the bird upwards. The size of the force on the air equals the size of the force on the bird; the direction of the force on the air (downwards) is opposite the direction of the force on the bird (upwards). For every action, there is an equal (in size) and opposite (in direction) reaction. Action-reaction force pairs make it possible for birds to fly.

Questions:



1.While driving down the road, a firefly strikes the windshield of a bus and makes a quite obvious mess in front of the face of the driver. This is a clear case of Newton's third law of motion. The firefly hit the bus and the bus hits the firefly. Which of the two forces is greater: the force on the firefly or the force on the bus?

Hint: Read Chapter again!

Answer

2. Many people are familiar with the fact that a rifle recoils when fired. This recoil is the result of action-reaction force pairs. A gunpowder explosion creates hot gases which expand outward allowing the rifle to push forward on the bullet. Consistent with Newton's third law of motion, the bullet pushes backwards upon the rifle. The acceleration of the recoiling rifle is ...

a. greater than the acceleration of the bullet.

b. smaller than the acceleration of the bullet.

c. the same size as the acceleration of the bullet.

Answer

Newton's second law of motion

Objects at equilibrium (the condition in which all forces balance) will not accelerate. According to Newton, an object will only accelerate if there is a net or unbalanced force acting upon it. The presence of an unbalanced force will accelerate an object - changing either its speed, its direction, or both its speed and direction.

Newton's second law of motion can be formally stated as follows:

When a net force acts on an object of constant mass, the object will accelerate and move in the direction of the resultant force.The product of the mass and acceleration of the object is equal to the resultant force.



Equation:

a = Fnet / m

Where,

a- acceleration
F- Force acting on object
m- mass

This equation can be rearranged to as follows:

Fnet = m * a

Fnet = m * g
(g - acceleration due to gravity)

(acceleration of free fall is due to Earth's gravity is 10(m/s)/s)

Hence,

W= m * g




The acceleration is directly proportional to the net force; the net force equals mass times acceleration; the acceleration in the same direction as the net force; an acceleration is produced by a net force. The NET FORCE. It is important to remember this distinction.


It is the net force which is related to acceleration.

*the net force is the vector sum of all the forces. If all the individual forces acting upon an object are known, then the net force can be determined.

Consistent with the above equation, a unit of force is equal to a unit of mass times a unit of acceleration. By substituting standard metric units for force, mass, and acceleration into the above equation, the following unit equivalency can be written.

Effect of forces on motion and Newton's First Law of motion

Effect of forces on motion:

1. a stationary objects to start moving (Movement)
2. Moving object to accelerate (Acceleration)
3. Moving object to decelerate (Deceleration)
4. Moving object to change direction(Direction)

Easy to remember:
Movement
Acceleration
Deceleration
Direction

*
Zero acceleration refers to objects that are stationary or moving with constant
velocity.In this case, different forces acting on it are balanced,add up to zero,
resultant or net force add up to zero.

Newton and his laws of motion

Isaac Newton (a 17th century scientist) put forth a variety of laws which explain why objects move (or don't move) as they do. These three laws have become known as Newton's three laws of motion.

Newton's First Law of motion(sometimes referred to as the law of inertia):

An object at rest tends to stay at rest and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an unbalanced force.

There are two parts to this statement - one which predicts the behavior of stationary objects and the other which predicts the behavior of moving objects. The two parts are summarized in the following diagram.




Example:

Suppose that you filled a baking dish to the rim with water and walked around an oval track making an attempt to complete a lap in the least amount of time. The water would have a tendency to spill from the container during specific locations on the track. In general the water spilled when:


* the container was at rest and you attempted to move it

* the container was in motion and you attempted to stop it

* the container was moving in one direction and you attempted to change its
direction.

The water spills whenever the state of motion of the container is changed. The water
resisted this change in its own state of motion.The container was moved from rest to a high speed at the starting line; the water remained at rest and spilled onto the table. The container was stopped near the finish line; the water kept moving and spilled over container's leading edge. The container was forced to move in a different direction to make it around a curve; the water kept moving in the same direction and spilled over its edge. The behavior of the water during the lap around the track can be explained by Newton's first law of motion.(Water keeps on doing what its doing)

More Examples:

*
Blood rushes from your head to your feet while quickly stopping when
riding on a descending elevator.

*
The head of a hammer can be tightened onto the wooden handle by banging the
bottom of the handle against a hard surface.

*
A brick is painlessly broken over the hand of a physics teacher by slamming it
with a hammer. (CAUTION: do not attempt this at home!)

*
To dislodge ketchup from the bottom of a ketchup bottle, it is often turned
upside down and thrusted downward at high speeds and then abruptly halted.

*
Headrests are placed in cars to prevent whiplash injuries during rear-end
collisions.

*
While riding a skateboard (or wagon or bicycle), you fly forward off the board
when hitting a curb or rock or other object which abruptly halts the motion of
the skateboard.

Vector Diagrams

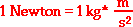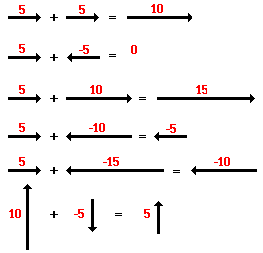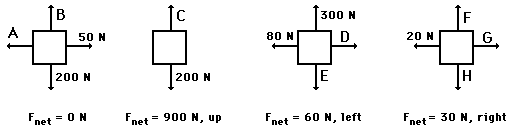
Vector Diagrams

Vector diagrams are diagrams which depict the direction and relative magnitude of a
vector quantity by a vector arrow. Vector diagrams can be used to describe the velocity of a moving object during its motion.

Vector diagrams can be used to represent any vector quantity.
For example, acceleration, force, and momentum.

How to draw a vector diagram?

A vector arrow is used to represent the direction and relative size of a quantity. It will become a very important representation of an object's motion.

*In a vector diagram, the magnitude of a vector quantity is represented by the size
of the vector arrow. If the size of the arrow in each consecutive frame of the vector diagram is the same, then the magnitude of that vector is constant.

A straght arrow represents a vector motion and its length represents its magnitude.
The direction of the force is represented by the direction in which the arrowhead points.

A scale is used to represent the magnitude of the vector
( Magnitude represented by the scale must be accurate)
The direction of the drawing must also be accurate.

Adding Vectors

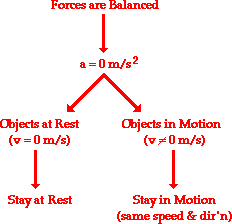
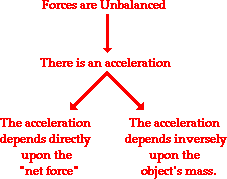
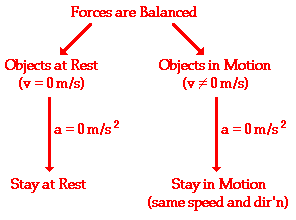
The net force is the vector sum of all the forces which act upon an object. That is to say, the net force is the sum of all the forces, taking into account the fact that a force is a vector and two forces of equal magnitude and opposite direction will cancel each other out.

The net force experienced by an object is determined by computing the vector sum of all the individual forces acting upon that object. That is the net force is the result(or resultant) of adding up all the force vectors to find a single vector that will produce the same effect as the two vectors added together.



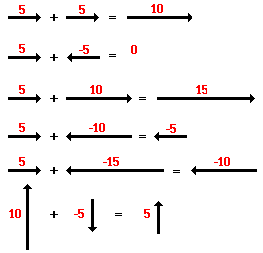
Observe in the diagram above that a downward vector will provide a partial or full cancellation of an upward vector. And a leftward vector will provide a partial or full cancellation of a rightward vector. The addition of force vectors can be done in the same manner in order to determine the net force (i.e., the vector sum of all the individual forces). Consider the three situations below in which the net force is determined by summing the individual force vectors which are acting upon the objects.



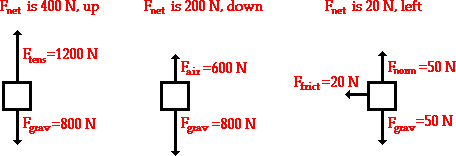
1. Free-body diagrams for four situations are shown below. For each situation, determine the net force acting upon the object. Click the buttons to view the answers.



Answer to situation A
The net force is zero Newtons. All the individual forces balance each other (i.e., cancel each other out).

Answer to situation B
The net force is 5 Newtons, left. The vertical forces balance each other (i.e., cancel each other out). The leftward force (friction) remains unbalanced.

Answer to situation C
The net force is zero Newtons. All the individual forces balance each other (i.e., cancel each other out).

Answer to situation D
The net force is 15 Newtons, up. The upward force of air resistance is only partially balanced by the downward force of gravity - 15 N of upward force remains unbalanced.

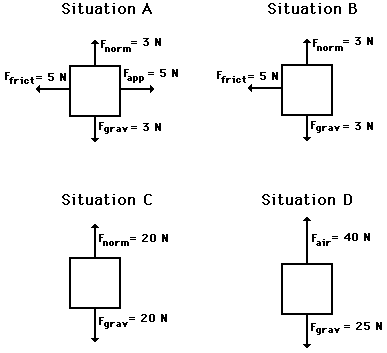
2. Free-body diagrams for four situations are shown below. The net force is known for each situation. However, the magnitudes of a few of the individual forces are not known. Analyze each situation individually and determine the magnitude of the unknown forces. Then click the button to view the answers.



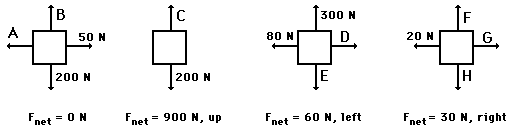See Answer

How to add non-parallel vectors?

There are two equivalent ways to add vectors graphically: the tip-to-tail method and the parallelogram method. Both will get you to the same result, but one or the other is more convenient depending on the circumstances.

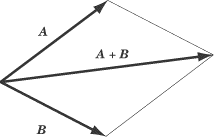
Tip-to-Tail Method
We can add any two vectors, A and B, by placing the tail of B so that it meets the tip of A. The sum, A + B, is the vector from the tail of A to the tip of B.



Note that you’ll get the same vector if you place the tip of B against the tail of A. In other words, A + B and B + A are equivalent.

Parallelogram Method
To add A and B using the parallelogram method, place the tail of B so that it meets the tail of A. Take these two vectors to be the first two adjacent sides of a parallelogram, and draw in the remaining two sides. The vector sum, A + B, extends from the tails of A and B across the diagonal to the opposite corner of the parallelogram. If the vectors are perpendicular and unequal in magnitude, the parallelogram will be a rectangle. If the vectors are perpendicular and equal in magnitude, the parallelogram will be a square.



Adding Vector Magnitudes
Of course, knowing what the sum of two vectors looks like is often not enough. Sometimes you’ll need to know the magnitude of the resultant vector. This, of course, depends not only on the magnitude of the two vectors you’re adding, but also on the angle between the two vectors.

Adding Perpendicular Vectors
Suppose vector A has a magnitude of 8, and vector B is perpendicular to A with a magnitude of 6. What is the magnitude of A + B? Since vectors A and B are perpendicular, the triangle formed by A, B, and A + B is a right triangle. We can use the Pythagorean Theorem to calculate the magnitude of A + B, which is



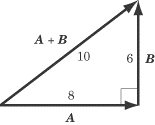
Adding Vectors at Other Angles
When A and B are neither perpendicular nor parallel, it is more difficult to calculate the magnitude of A + B because we can no longer use the Pythagorean Theorem. It is possible to calculate this sum using trigonometry, but SAT II Physics will never ask you to do this. For the most part, SAT II Physics will want you to show graphically what the sum will look like, following the tip-to-tail or parallelogram methods. On the rare occasions that you need to calculate the sum of vectors that are not perpendicular, you will be able to use the component method of vector addition, explained later in this chapter.

Example

Vector A has a magnitude of 9 and points due north, vector B has a magnitude of 3 and points due north, and vector C has a magnitude of 5 and points due west. What is the magnitude of the resultant vector, A + B + C?
First, add the two parallel vectors, A and B. Because they are parallel, this is a simple matter of straightforward addition: 9 + 3 = 12. So the vector A + B has a magnitude of 12 and points due north. Next, add A + B to C. These two vectors are perpendicular, so apply the Pythagorean Theorem:
The sum of the three vectors has a magnitude of 13. Though a little more time-consuming, adding three vectors is just as simple as adding two.

Forces

What is a force?

A force is a push or pull that one object exerts on another.
It produces or tends to produce motion, and stops or tends to stop motion.


Types of forces (7 types):

1. Contact Force - push experienced by two objects pressed together.
2. Weight - gravitational pull of the earth on an object
3. Friction - motion opposing force that exsit when surface of two objects move
against each other.
4. Tension - pull at both ends of a sting, spring or rope
5. Resistance - a type of force existing in fluids giving a viscous effect
See website for general information:
(http://www.millersville.edu/~jdooley/macro/derive/viscous/visplat/visplat.htm)
6. Electric Force - push or pull between electric charges
7. Magnetic Force - push or pull between magnets or magnets and magnetic materials

S.I. unit of force is newtons(N)

1N - amount of gravitational force acting on 100g mass
1N is defined as a force that produces acceleration of (1m/s)/s on a mass of 1kg




Activity:

Object Melon Apple Pat Eatladee Fred

Mass (kg) 1 kg Ans(b) 25 kg Ans(c)

Weight (N) Ans(a) 0.98 N Ans(d) 980 N

(a)9.8 N (or ~10 N if approximating g to be 10 m/s/s)
(b)0.1 kg (or ~0.098 kg if approximating g to be 10 m/s/s)
(c)245 N (or ~250 N if approximating g to be 10 m/s/s)
(d)100 kg (or ~98 kg if approximating g to be 10 m/s/s)



2. Different masses are hung on a spring scale calibrated in Newtons.

1. The force exerted by gravity on 1 kg = 9.8 N.
2. The force exerted by gravity on 5 kg = ______ N.
3. The force exerted by gravity on _______ kg = 98 N.
4. The force exerted by gravity on 70 kg = ________ N.

See Answer