A series circuits has only one path for electrons through which electric charge can flow.

Current in Series circuit
The amount of current is the same through any component in the circuit.This is because there is only one path for electrons to flow in a series circuit, and because free electrons flow through conductors like marbles in a tube, the rate of flow (marble speed) at any point in the circuit (tube) at any specific point in time must be equal.
Charge does NOT become used up by resistors such that there is less of it at one location compared to another.
Ibattery = I1 = I2 = I3 = ...
where I1, I2, and I3 are the current values at the individual resistor locations.
These current values are easily calculated if the battery voltage is known and the individual resistance values are known. Using the individual resistor values and the equation above, the equivalent resistance can be calculated. And using Ohm's law (V = I • R), the current in the battery and thus through every resistor can be determined by finding the ratio of the battery voltage and the equivalent resistance.
Ibattery = I1 = I2 = I3 =  Vbattery / Req
Vbattery / Req
Resistance in Series Current
The actual amount of current varies inversely with the amount of overall resistance. There is a clear relationship between the resistance of the individual resistors and the overall resistance of the collection of resistors. As far as the battery that is pumping the charge is concerned, the presence of two 6-
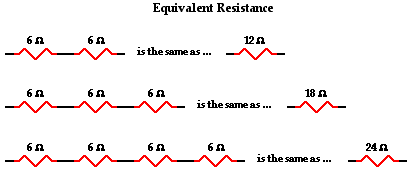
This is the concept of equivalent resistance. The equivalent resistance of a circuit is the amount of resistance that a single resistor would need in order to equal the overall affect of the collection of resistors that are present in the circuit. For series circuits, the mathematical formula for computing the equivalent resistance (Req) is
Req = R1 + R2 + R3 + ...
where R1, R2, and R3 are the resistance values of the individual resistors that are connected in series.
Electric Potential Difference and Voltage Drops
The electrochemical cell of a circuit supplies energy to the charge to move it through the cell and to establish an electric potential difference across the two ends of the external circuit. A 1.5-volt cell will establish an electric potential difference across the external circuit of 1.5 volts. This is to say that the electric potential at the positive terminal is 1.5 volts greater than at the negative terminal. As charge moves through the external circuit, it encounters a loss of 1.5 volts of electric potential. This loss in electric potential is referred to as a voltage drop. It occurs as the electrical energy of the charge is transformed to other forms of energy (thermal, light, mechanical, etc.) within the resistors or loads. If an electric circuit powered by a 1.5-volt cell is equipped with more than one resistor, then the cumulative loss of electric potential is 1.5 volts. There is a voltage drop for each resistor, but the sum of these voltage drops is 1.5 volts - the same as the voltage rating of the power supply.
This concept can be expressed mathematically by the following equation:
Parallel Circuits
In a parallel arrangement, there is more than one path through which electric charge can flow.
Current in Parallel Circuits
he current divides to flow through each of the components in the parallel paths. The amount of current that flows through each of the components depends on the resistance of each component. A component with a lower resistance will allow more current to flow through.
The current outside the branches is the same as the sum of the current in the individual branches. It is still the same amount of current, only split up into more than one pathway.

In equation form, this principle can be written as
Itotal = I1 + I2 + I3 + ...
where Itotal is the total amount of current outside the branches (and in the battery) and I1, I2, and I3 represent the current in the individual branches of the circuit.
Resistance in Parallel Circuit
The actual amount of current always varies inversely with the amount of overall resistance. There is a clear relationship between the resistance of the individual resistors and the overall resistance of the collection of resistors.
To explore this relationship, let's begin with the simplest case of two resistors placed in parallel branches, each having the same resistance value of 4 . Since the circuit offers two equal pathways for charge flow, only one-half the charge will choose to pass through a given branch.
While each individual branch offers 4 of resistance to any charge that flows through it, only one-half of all the charge flowing through the circuit will encounter the 4 resistance of that individual branch. Thus, as far as the battery that is pumping the charge is concerned, the presence of two 4- resistors in parallel would be equivalent to having one 2- resistor in the circuit.
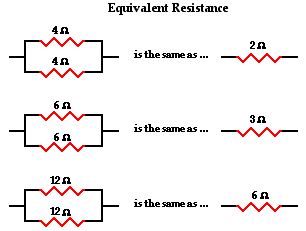
This is the concept of equivalent resistance. The equivalent resistance of a circuit is the amount of resistance that a single resistor would need in order to equal the overall effect of the collection of resistors that are present in the circuit. For parallel circuits, the mathematical formula for computing the equivalent resistance (Req) is
1 / Req = 1 / R1 + 1 / R2 + 1 / R3 + ...
where R1, R2, and R3 are the resistance values of the individual resistors that are connected in parallel. The examples above could be considered simple cases in which all the pathways offer the same amount of resistance to an individual charge that passes through it. The simple cases above were done without the use of the equation. Yet the equation fits both the simple cases where branch resistors have the same resistance values and the more difficult cases where branch resistors have different resistance values. For instance, consider the application of the equation to the one simple and one difficult case below.
Example : Three 12 resistors are placed in parallel
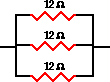
1/Req = 1/R1 + 1/R2 + 1/R3
1/Req = 1/(12 ![]() ) + 1/(12
) + 1/(12 ![]() ) + 1/(12
) + 1/(12 ![]() )
)
Using a calculator ...
1/Req = 0.25 ![]() -1
-1
Req = 1 / (0.25 ![]() -1)
-1)
Req = 4.0 ![]()
 Vbattery =
Vbattery =  V1 =
V1 =  V2 =
V2 =  V3 = ...
V3 = ...
If three resistors are placed in parallel branches and powered by a 12-volt battery, then the voltage drop across each one of the three resistors is 12 volts. A charge flowing through the circuit would only encounter one of these three resistors and thus encounter a single voltage drop of 12 volts.
Summary
Series Circuits
- The current is the same in every resistor; this current is equal to that in the battery.
- The sum of the voltage drops across the individual resistors is equal to the voltage rating of the battery.
- The overall resistance of the collection of resistors is equal to the sum of the individual resistance values,
Parallel Circuits
- The voltage drop is the same across each parallel branch.
- The sum of the current in each individual branch is equal to the current outside the branches.
- The equivalent or overall resistance of the collection of resistors is given by the equation
1/Req = 1/R1 + 1/R2 + 1/R3 ...
I can’t wait to read more of your works. Having read this I believe it’s beneficial and insightful. Cheers!
ReplyDeletewww.n8fan.net
Great! Really helped me understand
ReplyDeleteGreat! Really helped me to understand
ReplyDelete