Pressure

Pressure

Pressure is the force on an object that is spread over a surface area.

The equation for pressure is the force divided by the area where the force is applied. Although this measurement is straightforward when a solid is pushing on a solid, the case of a solid pushing on a liquid or gas requires that the fluid be confined in a container. The force can also be created by the weight of an object.

The smaller the sufface area, the greater is the pressure. This is because the force is spread over a smaller area.

Pressure of solid on a solid

When you apply a force to a solid object, the pressure is defined as the force applied divided by the area of application.Hence,

Pressure depends on two things:

* the Force (in Newtons) and

* the Area it's pressing on (in square metres)

The equation for pressure is:

P = F/A

where

* P is the pressure
* F is the applied force
* A is the surface area where the force is applied
* F/A is F divided by A

The unit of pressure is the pascal

1 Pascal means 1 Newton per square metre
So, 1 Pa = 1 N m-2.
Another unit of pressure that is used is bar. Note that 1 bar = 105 Pa and 1 bar = 1000 millibars.

The pascal is also a unit of stress and the topics of pressure and stress are connected.

* Bed of nails (not really pressure but shear strain?)
* Finger bones are flat on the gripping side to increase surface area in contact and thus reduce compressional stresses

Pressure is isotropic, which means that it acts equally in all directions.
Thus, liquids exert the same pressure in all directions at a given depth.

For example, if you push on an object with your hand with a force of 20 pounds, and the area of your hand is 10 square inches, then the pressure you are exerting is
20 / 10 = 2 pounds per square inch.



You can see that for a given force, if the surface area is smaller, the pressure will be greater. If you use a larger area, you are spreading out the force, and the pressure (or force per unit area) becomes smaller.

Here's an example:

The force on the bench is the weight of the block: 80 N
The area it's pressing on is the base area of the block which is 2 square metres.

So the pressure on the bench is

80 ÷ 2 = 40 Pascals

Notice that a large force might only create a small pressure if it's spread out over a wide area.Also, a small force can create a big pressure if the area is tiny.

Try these Questions:

1) An office safe has a weight of 500N. If the area of the base is 1.25 square metres, what is the pressure on the floor of the office?

Answer

2) A physics teacher has a weight of 800N. If his feet have an area of 0.025 square metres each, what pressure does he exert on the ground? (Remember, he has two feet!)

Answer

Some Applications of Pressure

Using Pressure

* When the area is small, a moderate force can create a very large pressure. This is why a sharp knife is good at cutting things: when you push the very small area of the sharp blade against something, it creates a really large pressure.

* Ice skates have sharp edges, and thus a small area in contact with the ice.
This means that your weight creates a very large pressure on the ice, far more than if you were standing in ordinary shoes.
Ice has an unusual property: it can melt under pressure, even if it's below 0°C. When you're ice skating, you're actually skating on a layer of water that you've just melted, which quickly re-freezes when you move on (you're not skating on ice at all!) This is called regelation, and means that there's very little friction as you skate along.

* Even a slender supermodel can damage floors by walking on then in high-heeled shoes. This is because the area of the heel is small, so you can easily create enough pressure to cause a dent in the floor.
The pressure can be greater than if an elephant was standing there, even though the force is much less. So you should be able to figure out why elephants and camels have large feet.

Power

Power

The quantity work has to do with a force causing a displacement. Work has nothing to do with the amount of time that this force acts to cause the displacement. Sometimes, the work is done very quickly and other times the work is done rather slowly.


For example, a rock climber takes an abnormally long time to elevate her body up a few meters along the side of a cliff. On the other hand, a trail hiker (who selects the easier path up the mountain) might elevate her body a few meters in a short amount of time. The two people might do the same amount of work, yet the hiker does the work in considerably less time than the rock climber. The quantity which has to do with the rate at which a certain amount of work is done is known as the power. The hiker has a greater power rating than the rock climber.



Power is the rate at which work is done. It is the work/time ratio. Mathematically, it is computed using the following equation.



The standard metric unit of power is the Watt. As is implied by the equation for power, a unit of power is equivalent to a unit of work divided by a unit of time. Thus, a Watt is equivalent to a Joule/second.

We can rearrange the equations:

W = Power x time
Energy = Power x time

1. Two physics students, Will N. Andable and Ben Pumpiniron, are in the weightlifting room. Will lifts the 100-pound barbell over his head 10 times in one minute; Ben lifts the 100-pound barbell over his head 10 times in 10 seconds. Which student does the most work? ______________ Which student delivers the most power? ______________ Explain your answers.


Answer



2. During a physics lab, Jack and Jill ran up a hill. Jack is twice as massive as Jill; yet Jill ascends the same distance in half the time. Who did the most work? ______________ Who delivered the most power? ______________ Explain your answers.



Answer



3. A tired squirrel (mass of approximately 1 kg) does push-ups by applying a force to elevate its center-of-mass by 5 cm in order to do a mere 0.50 Joule of work. If the tired squirrel does all this work in 2 seconds, then determine its power.


Answer



4. When doing a chin-up, a physics student lifts her 42.0-kg body a distance of 0.25 meters in 2 seconds. What is the power delivered by the student's biceps?



Answer


5. Your household's monthly electric bill is often expressed in kilowatt-hours. One kilowatt-hour is the amount of energy delivered by the flow of l kilowatt of electricity for one hour. Use conversion factors to show how many joules of energy you get when you buy 1 kilowatt-hour of electricity.



Answer



6. An escalator is used to move 20 passengers every minute from the first floor of a department store to the second. The second floor is located 5.20 meters above the first floor. The average passenger's mass is 54.9 kg. Determine the power requirement of the escalator in order to move this number of passengers in this amount of time.


Answer

Work Done

Work Done



When a force acts upon an object to cause a displacement of the object, it is said that work was done upon the object. There are three key ingredients to work - force, displacement, and cause. In order for a force to qualify as having done work on an object, there must be a displacement and the force must cause the displacement

"Work done" is another way of saying "energy transferred".
Work done = Energy transferred.
W = E

The equation which connects work, force and distance is

Work done = Force x Distance.
W = F x d



The equation can also be written as

Energy = Force x Distance.

E = F x d

In words:

Work done by a constant force on an object is given by the product of the force and the distancce moved by the object in the direction of the force.

Whenever a new quantity is introduced in physics, the standard metric units associated with that quantity are discussed. In the case of work (and also energy), the standard metric unit is the Joule (abbreviated J). One Joule is equivalent to one Newton of force causing a displacement of one meter. In other words,
The Joule is the unit of work.
1 Joule = 1 Newton * 1 meter
1 J = 1 N * m

Cases where no work is done:

1. Work is not done when The direction of the applied force and the direction in which the object moves are perpendicular to each other.
2.Work is zero if applied force is zero (W=0 if F=0): If a block is moving on a smooth horizontal surface (frictionless), no work will be done. Note that the block may have large displacement but no work gets done.
3.Work done is zero when displacement is zero. This happens when a man pushes a wall. There is no displacement of the wall. Thus, there is no work done.

In order to accomplish work on an object there must be a force exerted on the object and it must move in the direction of the force.



In summary, work is done when a force acts upon an object to cause a displacement. Three quantities must be known in order to calculate the amount of work. Those three quantities are force, displacement and the angle between the force and the displacement.

MECHANICAL ENERGY



In the process of doing work, the object which is doing the work exchanges energy with the object upon which the work is done. When the work is done upon the object, that object gains energy. The energy acquired by the objects upon which work is done is known as mechanical energy.
The two types of Mechanical energy that a body may have are Kinetic Energy and Gravitational Potential energy.

Kinetic Energy


Kinetic energy is the energy of motion. An object which has motion - whether it be vertical or horizontal motion - has kinetic energy. Whereas An Object which is stationary does not have any kinetic energy. When a force moves an object, it does work and it gains kinetic energy.
Hence, we can see that the kinetic energy of the object is due to the work done by the force.


The amount of translational kinetic energy (from here on, the phrase kinetic energy will refer to translational kinetic energy) which an object has depends upon two variables: the mass (m) of the object and the speed (v) of the object. The following equation is used to represent the kinetic energy (KE) of an object.



where m = mass of object

v = speed of object

This equation reveals that the kinetic energy of an object is directly proportional to the square of its speed.

Kinetic energy is a scalar quantity; it does not have a direction. Unlike velocity, acceleration, force, and momentum, the kinetic energy of an object is completely described by magnitude alone.

Like work and potential energy, the standard metric unit of measurement for kinetic energy is the Joule. As might be implied by the above equation, 1 Joule is equivalent to 1 kg*(m/s)^2.



We can see that for two objects of the same mass moving at different speeds ,the faster object has a greater kinetic energy.Similarly, for two objects of different masses moving at different speeds, the object of greater mass has greater kinetic energy.

Check Your Understanding

1. Determine the kinetic energy of a 625-kg roller coaster car that is moving with a speed of 18.3 m/s.

Answer

2. If the roller coaster car in the above problem were moving with twice the speed, then what would be its new kinetic energy?

Answer

3. Missy Diwater, the former platform diver for the Ringling Brother's Circus, had a kinetic energy of 12 000 J just prior to hitting the bucket of water. If Missy's mass is 40 kg, then what is her speed?


Answer

4. A 900-kg compact car moving at 60 mi/hr has approximately 320 000 Joules of kinetic energy. Estimate its new kinetic energy if it is moving at 30 mi/hr. (HINT: use the kinetic energy equation as a "guide to thinking.")

Answer

Potential Energy

An object can store energy as the result of its position. For example, the heavy heavy ball of a demolition machine is storing energy when it is held at an elevated position. This stored energy of position is referred to as potential energy.

Similarly, a drawn bow is able to store energy as the result of its position. When assuming its usual position (i.e., when not drawn), there is no energy stored in the bow.

Yet when its position is altered from its usual equilibrium position, the bow is able to store energy by virtue of its position. This stored energy of position is referred to as potential energy. Potential energy is the stored energy of position possessed by an object.

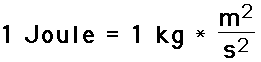
border="0" alt="" />

Gravitational Potential Energy

The two examples above illustrate the two forms of potential energy to be discussed in this course - gravitational potential energy and elastic potential energy. Gravitational potential energy is the energy stored in an object as the result of its vertical position or height. The energy is stored as the result of the gravitational attraction of the Earth for the object. The gravitational potential energy of the massive ball of a demolition machine is dependent on two variables - the mass of the ball and the height to which it is raised. There is a direct relation between gravitational potential energy and the mass of an object.

These relationships are expressed by the following equation:

PEgrav = mass * g * height
PEgrav = m * g * h



In the above equation, m represents the mass of the object, h represents the height of the object and g represents the acceleration of gravity (9.8 m/s/s on Earth).

More massive objects have greater gravitational potential energy. There is also a direct relation between gravitational potential energy and the height of an object. The higher that an object is elevated, the greater the gravitational potential energy.

Since the gravitational potential energy of an object is directly proportional to its height above the zero position, a doubling of the height will result in a doubling of the gravitational potential energy. A tripling of the height will result in a tripling of the gravitational potential energy.


Use this principle to determine the blanks in the following diagram. Knowing that the potential energy at the top of the tall platform is 50 J, what is the potential energy at the other positions shown on the stair steps and the incline?




ANS



1. A cart is loaded with a brick and pulled at constant speed along an inclined plane to the height of a seat-top. If the mass of the loaded cart is 3.0 kg and the height of the seat top is 0.45 meters, then what is the potential energy of the loaded cart at the height of the seat-top?


ANS

2.2. If a force of 14.7 N is used to drag the loaded cart (from previous question) along the incline for a distance of 0.90 meters, then how much work is done on the loaded cart?